Paraguas
Este proyecto tiene como objetivo que aprendas a construir un objeto que simula el funcionamiento de un paraguas.
Con ello podrás aprender cómo a través de los Alquimétricos se pueden diseñar, imitar o replicar mecanismos que se encuentran presentes en diversos objetos de uso cotidiano, gracias a la versatilidad que tiene Alquimétricos para combinar sus encastres.
MATERIALES NECESARIOS
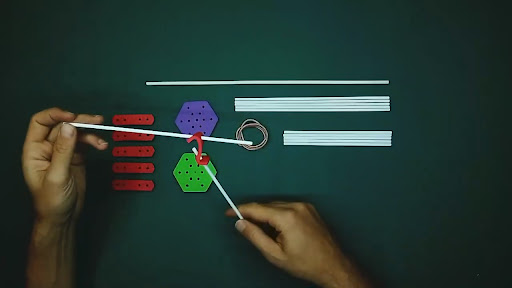
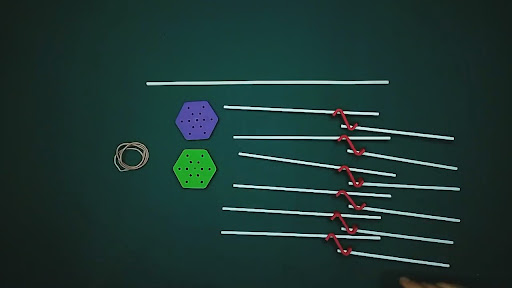
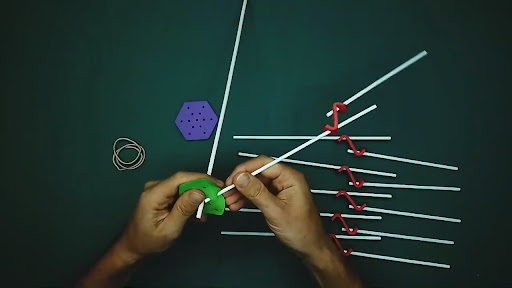
- 2 Conectores hexagonales
- 6 Conectores lineales
- 13 varillas de largos variables
- 6 varillas de 15 cm (rayos)
- 6 varillas de 22 cm (costillas)
- 1 varilla de > 35 cm (bastón)
- 1 Bandita elástica
BAJAR CONTENIDOS
Ingrese para bajar los contenidos
FICHA TÉCNICA
- Duración: 60´
- Área: Ciencias // Matemática // Arte
- Nivel de dificultad: Medio//Alto
- Edad: 8+
- Licencia: Creative Commons 4.0 atribución.
- Créditos: Tati Tabak, Fernando Daguanno, Carlos Vidal, Luciana Squeri, Léo Melo, Alquimétricos 2020/2021
PRERREQUISITOS
- ANTES DE COMENZAR
Todo lo que precisas saber para elegir y utilizar correctamente los materiales y herramientas necesarios para hacer tus Alquimétricos. - REPRODUCIR MOLDES
En el caso de que no tengas cómo imprimir el diseño de los moldes provistos. - FABRICAR MOLDES
Siempre es bueno tener distintos moldes listos antes de comenzar a profucir conectores. - FABRICAR CONECTORES
El bloque fundamental de toda construcción alquimétrica son los conectores y las varillas. La salsa secreta está aquí… - ENCASTRES
Conoce y experimenta con las diferentas formas de vincular conectores y varillas, o crea las tuyas y compártelas aquí.
CONTENIDOS CURRICULARES
Paso a paso
1
Agujerear con el sacabocado el centro de ambos conectores hexagonales
2
Pasar una varilla costilla (la de 22 cm) por dos de los orificios de un conector lineal, de forma cóncava.
3
Pasar un varilla rayo (una de 15 cm) por los otros dos orificios del mismo conector lineal, pero esta vez de modo convexo.
El conector lineal debe quedar como una S.
4
Repetir de forma similar los pasos 2 y 3 con todos los conectores lineales restantes.
5
Hacer un tope con una bandita elástica cercana a uno de los extremos de la varilla bastón (35 cm)
6
Colocar uno de los hexágonos (el verde) en la parte más corta de la varilla bastón por el agujero central que se hizo en el paso 1, hasta trabar con el tope.
7
Insertar al hexágono verde del paso 6, las estructuras lineales hechas al inicio del lado de la varilla costilla (22 cm) de forma cóncava.
8
Repetir esta acción con las otras 6 estructuras lineales.
9
Colocar el segundo hexágono (el lila) en la varilla bastón y correrla aproximadamente hasta la mitad, por el agujero central que se hizo en el paso 1.
10
Colocar las 6 estructuras lineales desde las varillas rayos (15 cm) en el hexágono lila del paso 9, de forma convexa.
11
Acercar de a dos los conectores lineales y asegurarse que estén a la misma distancia.
12
Opcional. Colocar desde la parte superior de la varilla bastón un círculo con su centro cortado, Puede ser de algún material flexible (tela, papel) y, si es necesario, previamente plegar de forma que se marquen 24 triángulos.
Trabar con el hexágono superior (el verde)
Para continuar aprendiendo
En casa
Se le pueden hacer distintas fundas al paragua, variando el tipo de material, el color, y observar las diferencias on respecto al paso de la luz o del agua.
Pueden colgarle en cada varilla tiras de papel en los bordes para decorarlo y realizar juegos y bailes inspirado en la forma en el que lo han decorado.
Pueden realizar dibujos en la parte interna de la cobertura del paragua, como por ejemplo un decorado similar el cielo, o gajos de diversos colores que al girarlos se superponen y se ven de otro color.
En la escuela
Pueden observar el paraguas y hallar todas las figuras planas que se observan, como por ejemplo triángulos, círculo, o las figuras que potencialmente se podrían observar, como un hexágono, y trabajar con las propiedades geométricas de esas figuras y la relaciones entre sí. Por ejemplo los triángulos simétricos que componen el posible hexágono, las varillas del paraguas, que si llegan hasta el borde exacto de la cubierta, representan los radios de la circunferencia,
Pueden colocar una hoja negra sobre una proyección del cielo, copiar con tiza algunas estrellas brillantes o concretamente las estrellas principales de alguna constelación elegida y realizarles orificios para luego utilizar de cobertura del paraguas estelar cada vez que se lo apunta a una luz. También se lo puede utilizar de noche haciéndola coincidir con la constelación real observada.
Pueden realizar un ejercicio matemático de proporcionalidad con el aumento o la reducción del tamaño de las varillas y posteriormente comparar el tamaño de la circunferencia de cobertura, para calcular si se amplía o se reduce con la misma relación de proporción, manteniendo su razón de cambio.
Pueden analizar la relación entre las propiedades de los materiales y la función dentro del objeto, observando, por ejemplo, la necesidad de las partes rígidas o flexibles. A su vez pueden modificar el material de la cubierta, por ejemplo para comparar materiales permeables, semipermeables e impermeables o para observar cuáles son transparentes, traslúcidos u opacos.
Pueden realizar una cobertura utilizando los colores del disco de newton o pares de colores complementarios y hacer girar el paraguas observando el color que se observa al hacerlo con cierta velocidad
Pueden decorar el paraguas y utilizarlo dentro de una coreografía o como elemento de una obra de teatro.
¿Sabías qué?
La Ravenala madagascariensis o árbol del viajero se llama así porque cualquier viajero sediento que se encontrara en la isla de Madagascar pueden encontrar agua depositada en muchas partes de la planta, como los foliolos de las hojas, las brácteas de las flores y en el interior de los huecos de la base de cada hoja.
Cada planta puede almacenar hasta un cuarto de litro de agua.
Cool!