Construir el icosaedro
¡Esta cápsula es para que aprendas a construir el icosaedro!
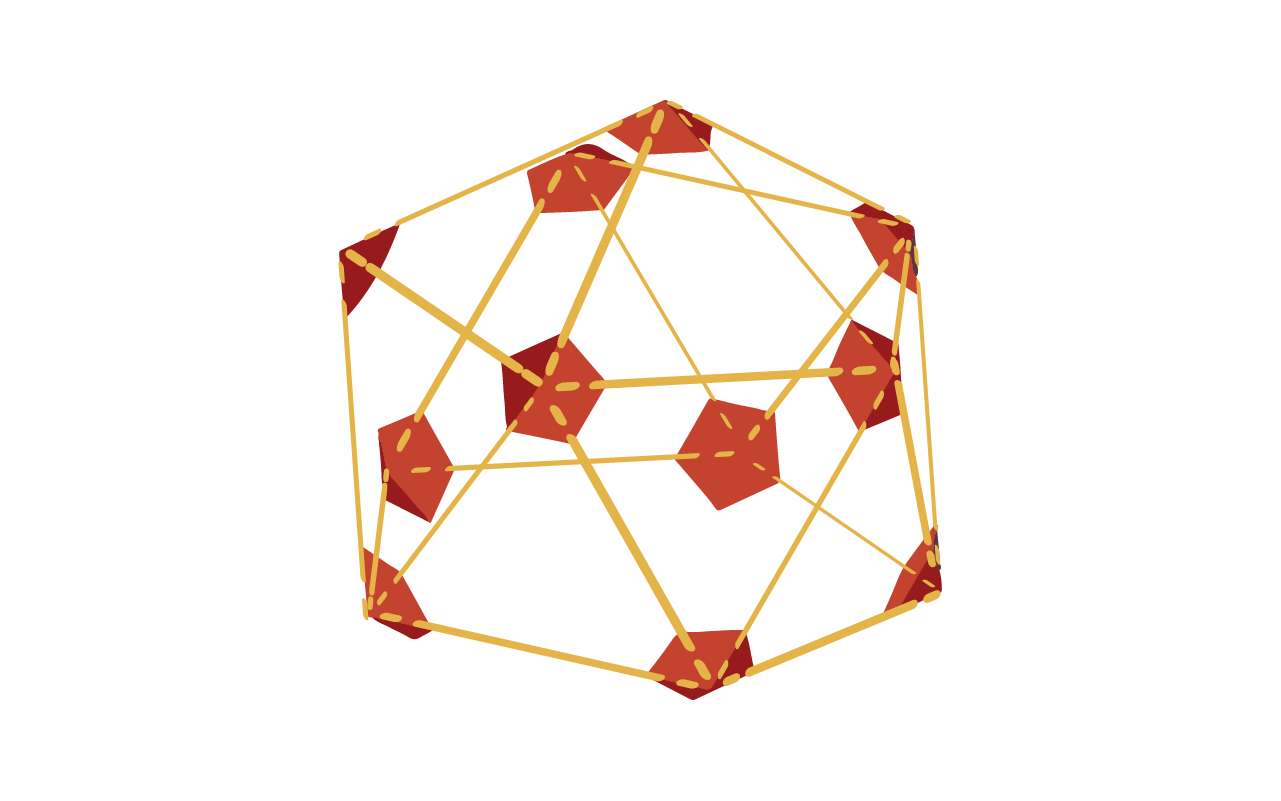
El sólido platónico más complejo tiene 30 aristas, 12 vértices y 20 caras. Debido a que tiene tantos componentes, parece una "bola" o esfera. De hecho, se suele utilizar como punto de partida para las cúpulas geodésicas, un tipo de estructura arquitectónica innovadora de formas redondeadas. Fueron desarrollados por el genio Buckminster Fuller a principios del siglo XX.
MATERIALES NECESARIOS
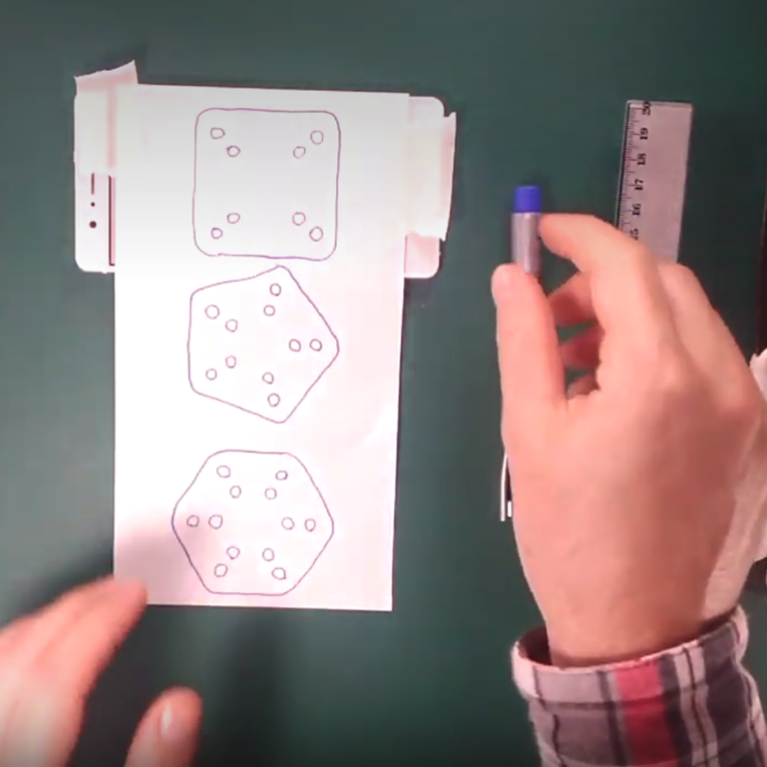
- 12 conectores pentagonales
- 30 varillas
- 60 gomas elásticas
Bajar contenidos.
FICHA TÉCNICA
- Duración: 45'
- Disciplina:
- Matemática –-
- Polígonos: clasificaciones en cuanto al número de vértices, las medidas de lados y ángulos y el paralelismo y perpendicularidad de los lados
- Relaciones entre arcos y ángulos en la circunferencia de un círculo
- Artes
- Elementos del lenguaje.
- Prácticas del lenguaje
- Producción de texto oral
- Producción de texto oral
-
- Nivel de deficultad: Medio.
- Licencia: Creative Commons 4.0 atribución.
- Créditos: Tati Tabak, Fernando Daguanno, Carlos Vidal, Luciana Squeri, Léo Melo, Alquimétricos 2020/2021
Prerrequisitos
- ANTES DE COMENZAR
Todo lo que precisas saber para elegir y utilizar correctamente los materiales y herramientas necesarios para hacer tus Alquimétricos. - REPRODUCIR MOLDES
En el caso de que no tengas cómo imprimir el diseño de los moldes provistos. - FABRICAR MOLDES
Siempre es bueno tener distintos moldes listos antes de comenzar a profucir conectores. - FABRICAR CONECTORES
El bloque fundamental de toda construcción alquimétrica son los conectores y las varillas. La salsa secreta está aquí… - ENCASTRES
Conoce y experimenta con las diferentas formas de vincular conectores y varillas, o crea las tuyas y compártelas aquí.
Contenidos curriculares
Acompaña el video
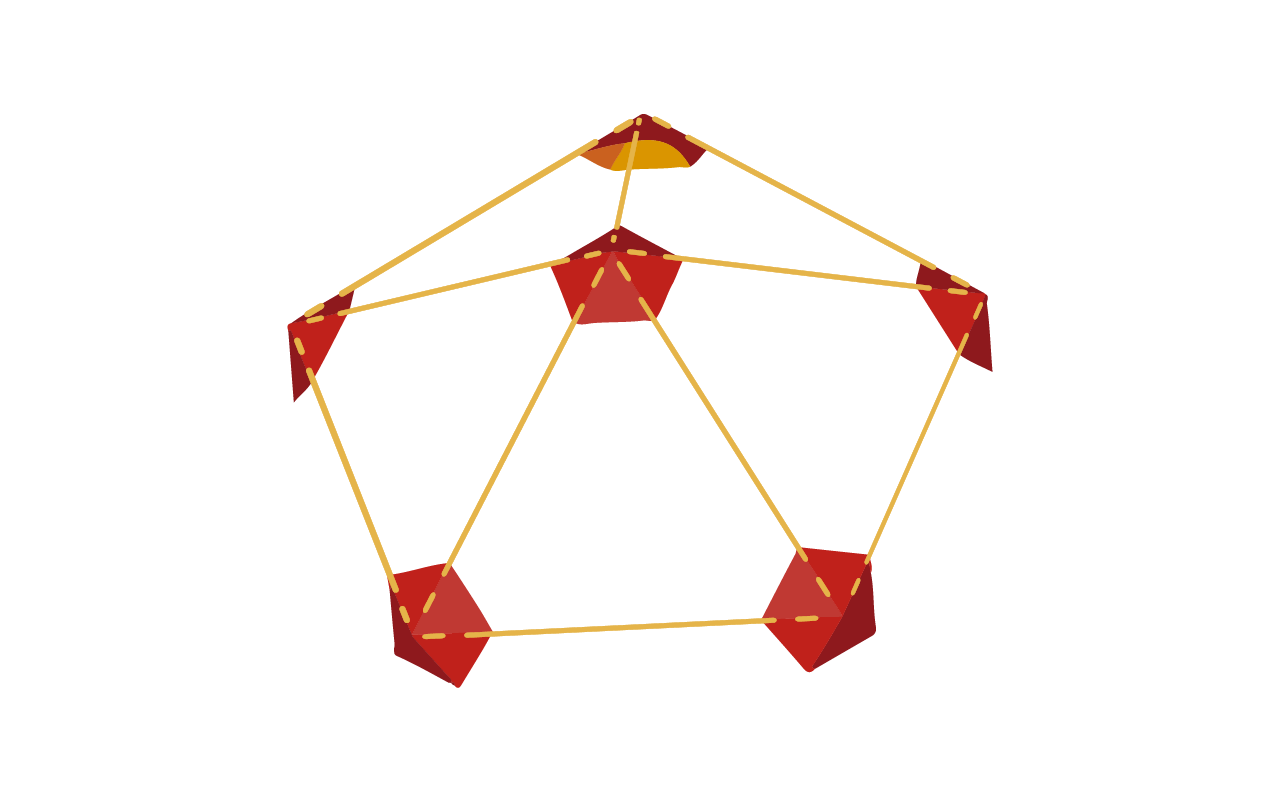
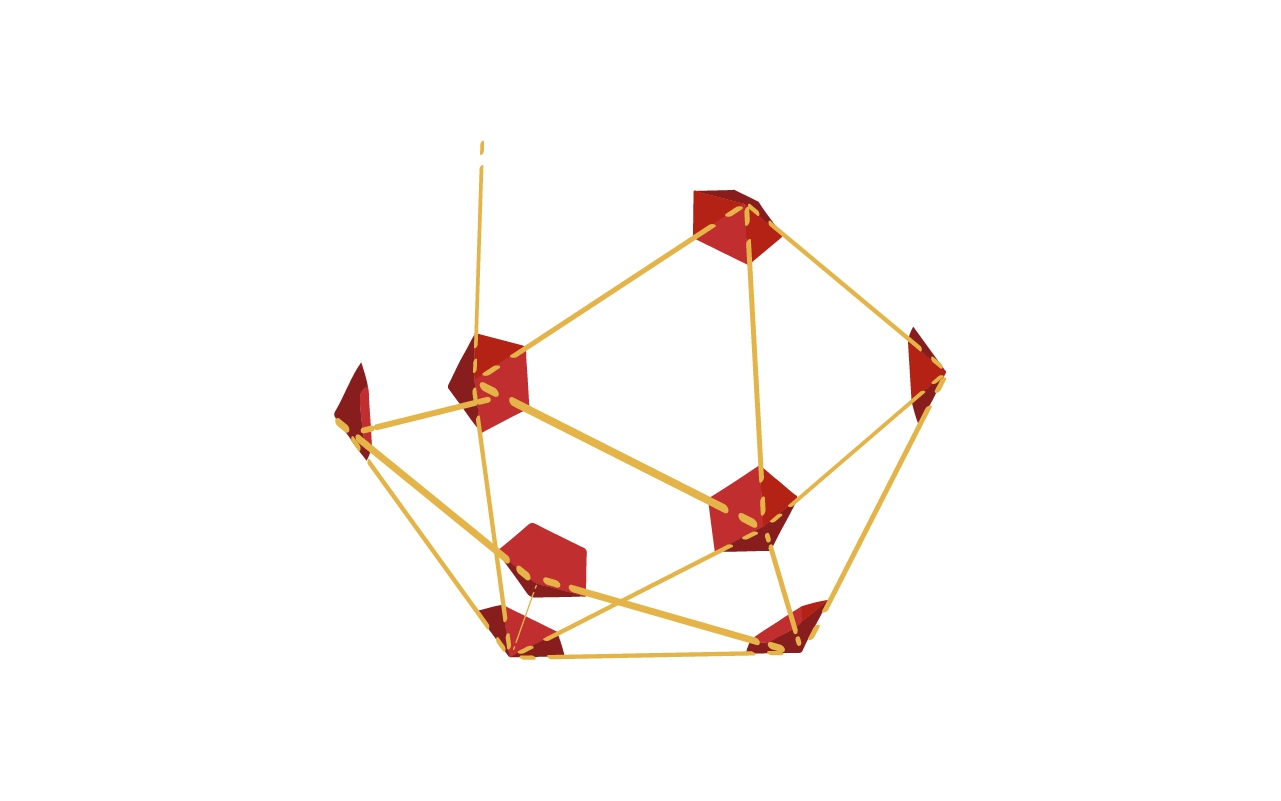
Observa con detalle un método de construcción del icosaedro desde un pentágono central, de forma espiralada.
Instrucciones paso a paso.
01
Tomar un conector pentagonal e insertar una varilla pasándola por los dos agujeros del alguno de los vértices. Entrando por encima de la figura y saliendo por debajo.
02
Pasar cuatro varillas más de la misma manera, completando todos los vértices del pentágono.
03
Colocar los conectores en los extremos libres de cada una de las cinco varillas usadas.
04
Unir dos conectores con cinco varillas nuevas, formando un pentágono. Utilice vértices adyacentes para pasar las varillas.
05
Colocar diez varillas en los dos vértices libres que dejó cada uno de los pentágonos.
06
Unir dos varillas más juntas con un nuevo conector, se necesitan un total de cinco.
07
Unir dos conectores con cinco varillas nuevas, formando un nuevo pentágono. Utilice vértices adyacentes para pasar las varillas a las utilizadas anteriormente.
Esta figura con base plana se llama domo geodésico.
08
Colocar las últimas 5 varillas en los únicos vértices libres que quedan en cada conector. Y únelos todos colocando el último conector pentagonal.
ATENCIÓN:
Recuerde que existe una alta posibilidad de que la varilla cortada se desprenda rápidamente al ser cortada, con el riesgo de lesionar a alguien o causar un problema. Puede intentar asegurarla ambos lados con los dedos o con ayuda para que no salga volando.
También puedes asegurarlas a la mesa con cinta adhesiva o pedirle a otra persona que te ayude a sostenerlas mientras los cortas.
Para continuar aprendiendo
Esta acción se puede utilizar para realizar ciertos cambios relacionados con:
Aproximaciones a la circunferencia.
- Reconocer algunos elementos que permiten una aproximación a la noción de esfera, tales como: cuerda, radio, diámetro.
- Relación con una pelota
Elementos gráficos de los cuerpos geométricos.
- Explorar, reconocer e identificar los elementos visuales: punto, línea, forma, espacio, relieve, movimiento, volumen bidimensional y tridimensional, tanto en la figura construida como en los objetos de la casa con los que se puede comparar dicha figura.
Lectura y escritura
- Es posible reflexionar sobre la importancia de identificar los aspectos centrales de una lista de pasos y probar las derivaciones de cambiar el orden de las instrucciones.
- Se pueden utilizar diferentes estrategias para la elaboración de instrucciones para el montaje del tetraedro, considerando diferentes situaciones y lectores.
